Page 102 - Spin Transport and Spintronics

4.1 ผลของอุณหภูมิที่มีต่อสภาพการนำไฟฟ้า 104

0.15
0.15 r ¯
0.12
0.12
(mW m) 0.09 r ­
0.09
0.06
r 0.06
r
0.03 ­¯
0.03
0 0
50 100 150 200 250 300 350 400
0 0 50 100 150 200 250 300 350 400
T (K)

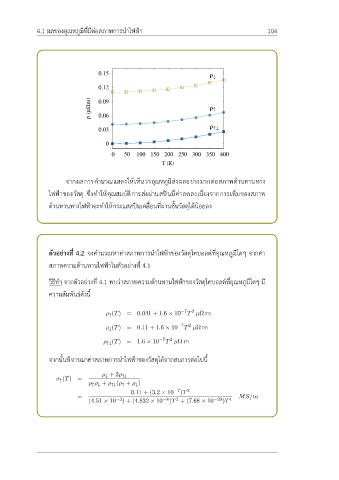
จากผลการคำนวณแสดงให้เห็นว่าอุณหภูมิส่งผลอย่างมากต่อสภาพต้านทานทาง

ไฟฟ้าของวัสดุ ซึ่งทำให้คุณสมบัติการส่งผ่านสปินมีค่าลดลงเนื่องจากการเพิ่มของสภาพ

ต้านทานทางไฟฟ้าจะทำให้กระแสสปินเคลื่อนที่ผ่านชั้นวัสดุได้น้อยลง

ตัวอย่างที่ 4.2 จงคำนวณหาค่าสภาพการนำไฟฟ้าของวัสดุโคบอลต์ที่อุณหภูมิใดๆ จากค่า

สภาพความต้านทานไฟฟ้าในตัวอย่างที่ 4.1

วิธีทำ จากตัวอย่างที่ 4.1 พบว่าสภาพความต้านทานไฟฟ้าของวัสดุโคบอลต์ที่อุณหภูมิใดๆ มี
ความสัมพันธ์ดังนี้

2
ρ ↑ (T) = 0.041 + 1.6 × 10 −7 T µΩ m
2
ρ ↓ (T) = 0.11 + 1.6 × 10 −7 T µΩ m
2
ρ ↑↓ (T) = 1.6 × 10 −7 T µΩ m

จากนั้นพิจารณาค่าสภาพการนำไฟฟ้าของวัสดุได้จากสมการต่อไปนี้

ρ ↓ + 2ρ ↑↓
σ ↑ (T) =
ρ ↑ ρ ↓ + ρ ↑↓ (ρ ↑ + ρ ↓ )
0.11 + (3.2 × 10 −7 )T 2
= MS/m
2
(4.51 × 10 −3 ) + (4.832 × 10 −8 )T + (7.68 × 10 −20 )T 4