Page 106 - Spin Transport and Spintronics

4.2 พารามิเตอร์สปินโพลาไรเซชัน 108

ρ 0↓ − ρ 0↑
β(T) =
ρ 0↓ + ρ 0↑ + 4ρ 0↑↓ + 6AT 2
2
′′
(ρ 0↓ − ρ 0↑ ) − β (ρ 0↓ + ρ 0↑ + 4ρ 0↑↓ + 6AT )
′
β (T) =
2
(ρ 0↓ + ρ 0↑ + 4ρ 0↑↓ + 6AT ) − β (ρ 0↓ − ρ 0↑ )
′′
N ↑ (E F )−N ↓ (E F ) = −0.724 จากนั้นนำค่าตัวแปรต่างๆ ที่โจทย์กำหนดให้ไป
′′
และค่า β =
N ↑ (E F )+N ↓ (E F )
แทนค่าในสมการข้างต้น จะได้ว่า
(0.11 − 0.041) 0.069
β(T) = =
0.11 + 0.041 + 6(1.6 × 10 −7 )T 2 0.151 + 9.6 × 10 −7 T 2
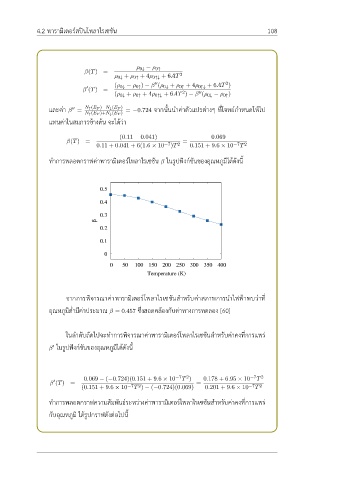
ทำการพลอตกราฟค่าพารามิเตอร์โพลาไรเซชัน β ในรูปฟังก์ชันของอุณหภูมิได้ดังนี้

0.5

0.4

0.3
b
0.2
0.1

0

0 50 100 150 200 250 300 350 400
Temperature (K)

จากการพิจารณาค่าพารามิเตอร์โพลาไรเซชันสำหรับค่าสภาพการนำไฟฟ้าพบว่าที่

อุณหภูมิต่ำมีค่าประมาณ β = 0.457 ซึ่งสอดคล้องกับค่าทางการทดลอง [60]

ในลำดับถัดไปจะทำการพิจารณาค่าพารามิเตอร์โพลาไรเซชันสำหรับค่าคงที่การแพร่

β ในรูปฟังก์ชันของอุณหภูมิได้ดังนี้
′

2
0.069 − (−0.724)(0.151 + 9.6 × 10 −7 T ) 0.178 + 6.95 × 10 −7 T 2
′
β (T) = =
2
(0.151 + 9.6 × 10 −7 T ) − (−0.724)(0.069) 0.201 + 9.6 × 10 −7 T 2
ทำการพลอตกราฟความสัมพันธ์ระหว่างค่าพารามิเตอร์โพลาไรเซชันสำหรับค่าคงที่การแพร่
กับอุณหภูมิ ได้รูปกราฟดังต่อไปนี้