Page 114 - Spin Transport and Spintronics

4.4 การคำนวณสปินทอร์ค 116

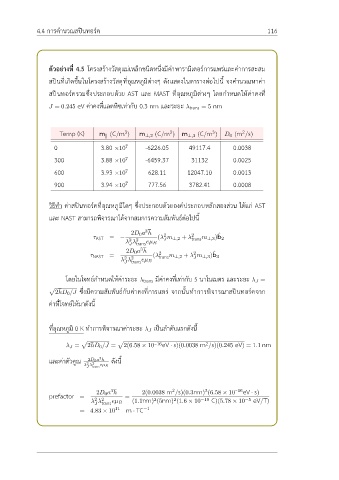
ตัวอย่างที่ 4.5 โครงสร้างวัสดุแม่เหล็กชนิดหนึ่งมีค่าพารามิเตอร์การแพร่และค่าการสะสม

สปินที่เกิดขึ้นในโครงสร้างวัสดุที่อุณหภูมิต่างๆ ดังแสดงในตารางต่อไปนี้ จงคำนวณหาค่า
สปินทอร์ครวมซึ่งประกอบด้วย AST และ MAST ที่อุณหภูมิต่างๆ โดยกำหนดให้ค่าคงที่

J = 0.245 eV ค่าคงที่แลตทิซเท่ากับ 0.3 nm และระยะ λtrans = 5 nm

3
3
3
2
Temp (K) m (C/m ) m ⊥,2 (C/m ) m ⊥,3 (C/m ) D 0 (m /s)
∥
0 3.80 ×10 7 -6226.05 49117.4 0.0038
300 3.88 ×10 7 -6459.37 31132 0.0025
600 3.93 ×10 7 628.11 12047.10 0.0013
900 3.94 ×10 7 777.56 3782.41 0.0008

วิธีทำ ค่าสปินทอร์คที่อุณหภูมิใดๆ ซึ่งประกอบด้วยองค์ประกอบหลักสองส่วน ได้แก่ AST

และ NAST สามารถพิจารณาได้จากสมการความสัมพันธ์ต่อไปนี้

3
2D 0 a ¯h 2 2
ˆ
τ AST = − (λ m ⊥,2 + λ trans m ⊥,3 )b 2
J
2
λ λ 2 eµ B
J trans
3
2D 0 a ¯h 2 2
ˆ
τ NAST = (λ trans m ⊥,2 + λ m ⊥,3 )b 3
J
2
λ λ 2 eµ B
J trans
โดยในโจทย์กำหนดให้ค่าระยะ λtrans มีค่าคงที่เท่ากับ 5 นาโนเมตร และระยะ λ J =
2¯hD 0 /J ซึ่งมีความสัมพันธ์กับค่าคงที่การแพร่ จากนั้นทำการพิจารณาสปินทอร์คจาก
p
ค่าที่โจทย์ให้มาดังนี้
ที่อุณหภูมิ 0 K ทำการพิจารณาค่าระยะ λ J เป็นลำดับแรกดังนี้

p p 2
−16
λ J = 2¯hD 0 /J = 2(6.58 × 10 eV · s)(0.0038 m /s)(0.245 eV) = 1.1nm
และค่าตัวคูณ 2D 0 a ¯h ดังนี้
3
2
λ λ 2 eµ B
J trans

2
3
3
−16
2D 0 a ¯h 2(0.0038 m /s)(0.3nm) (6.58 × 10 eV · s)
prefactor = =
2
−5
2
2
λ λ 2 eµ B (1.1nm) (5nm) (1.6 × 10 −19 C)(5.78 × 10 eV/T)
J trans
= 4.83 × 10 11 m · TC −1