Page 199 - Spin Transport and Spintronics
P. 199
7.3 ค่าคงที่ความหน่วงประสิทธิผล 201
อย่างไรก็ตามในกรณีชั้นฟิล์มบาง เราจะไม่พบความความสัมพันธ์แบบเชิงเส้นดังกล่าว ซึ่งผล
การคำนวณนี้ให้ผลที่สอดคล้องเป็นอย่างดีกับผลการทดลองซึ่งเป็นการยืนยันความถูกต้องของแบบ
จำลองระดับอะตอมในการคำนวณค่าคงที่ความหน่วง จากที่กล่าวมาข้างต้นเป็นการแสดงการคำนวณ
และอธิบายผลของค่าคงที่ความหน่วงประสิทธิผลซึ่งจะถูกนำไปใช้ในการออกแบบ STT-MRAM โดย
ในการออกแบบ STT-MRAM ควรใช้วัสดุที่มีค่าคงที่ความหน่วงที่ต่ำเนื่องจากจะช่วยให้การทำงานของ
STT-MRAM ใช้พลังงานต่ำ และจากการศึกษาพบว่าค่าคงที่ความหน่วงประสิทธิผลที่อุณหภูมิ 300 K
จะมีการลดลงตามความหนาของวัสดุ CoFeB ที่เพิ่มขึ้นซึ่งสอดคล้องกับผลการทดลอง นอกจากนี้พบ
ว่าค่าคงที่ความหน่วงของวัสดุ CoFeB ที่เหมาะสมสำหรับการนำไปใช้ในแบบจำลองในระดับตอมควร
มีค่าเท่ากับ 0.11 สำหรับชั้นรอยต่อและ 0.003 ที่ชั้นเบ้าค์ และค่าคงที่ความหน่วงของชั้นรอยต่อและ
ชั้นเบ้าค์ดังกล่าวจะถูกนำไปใช้ในการศึกษาการกลับทิศทางของแมกนีไทเซชันของโครงสร้าง CoFeB/
MgO/CoFeB ซึ่งจะอธิบายรายละเอียดในหัวข้อถัดไป
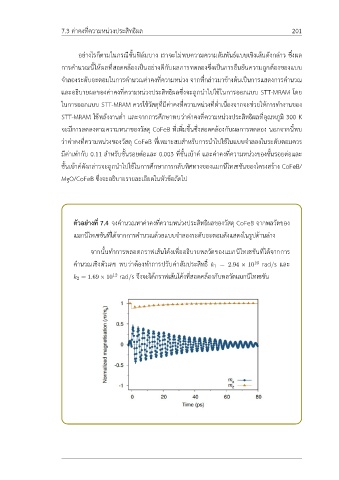
ตัวอย่างที่ 7.4 จงคำนวณหาค่าคงที่ความหน่วงประสิทธิผลของวัสดุ CoFeB จากพลวัตของ
แมกนีไทเซชันที่ได้จากการคำนวณด้วยแบบจำลองระดับอะตอมดังแสดงในรูปด้านล่าง
จากนั้นทำการพลอตกราฟเส้นโค้งเพื่ออธิบายพลวัตของแมกนีไทเซชันที่ได้จากการ
คำนวณเชิงตัวเลข พบว่าต้องทำการปรับค่าสัมประสิทธิ์ k 1 = 2.94 × 10 rad/s และ
10
k 2 = 1.69 × 10 rad/s จึงจะได้กราฟเส้นโค้งที่สอดคล้องกับพลวัตแมกนีไทเซชัน
12