Page 108 - Spin Transport and Spintronics
P. 108
4.3 ระยะการแพร่ของสปินและค่าคงที่การแพร่ 110
ร้อน เนื่องจากเมื่ออุณหภูมิของระบบมีค่าเพิ่มสูงขึ้นจะทำให้เกิดการลดลงของสภาพการนำไฟฟ้า [60]
ดังแสดงในรูปที่ 4.1
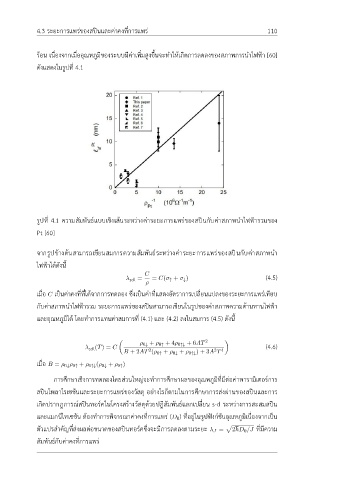
รูปที่ 4.1 ความสัมพันธ์แบบเชิงเส้นระหว่างค่าระยะการแพร่ของสปินกับค่าสภาพนำไฟฟ้ารวมของ
Pt [60]
จากรูปข้างต้นสามารถเขียนสมการความสัมพันธ์ระหว่างค่าระยะการแพร่ของสปินกับค่าสภาพนำ
ไฟฟ้าได้ดังนี้
C
λ sdl = = C(σ ↑ + σ ↓ ) (4.5)
ρ
เมื่อ C เป็นค่าคงที่ที่ได้จากการทดลอง ซึ่งเป็นค่าที่แสดงอัตราการเปลี่ยนแปลงของระยะการแพร่เทียบ
กับค่าสภาพนำไฟฟ้ารวม ระยะการแพร่ของสปินสามารถเขียนในรูปของค่าสภาพความต้านทานไฟฟ้า
และอุณหภูมิได้ โดยทำการแทนค่าสมการที่ (4.1) และ (4.2) ลงในสมการ (4.5) ดังนี้
2
ρ 0↓ + ρ 0↑ + 4ρ 0↑↓ + 6AT
λ sdl (T) = C (4.6)
2
2
B + 2AT (ρ 0↑ + ρ 0↓ + ρ 0↑↓ ) + 3A T 4
เมื่อ B = ρ 0↓ ρ 0↑ + ρ 0↑↓ (ρ 0↓ + ρ 0↑ )
การศึกษาเชิงการทดลองโดยส่วนใหญ่จะทำการศึกษาผลของอุณหภูมิที่มีต่อค่าพารามิเตอร์การ
สปินโพลาไรเซชันและระยะการแพร่ของวัสดุ อย่างไรก็ตามในการศึกษาการส่งผ่านของสปินและการ
เกิดปรากฎการณ์สปินทอร์คในโครงสร้างวัสดุด้วยปฎิสัมพันธ์แลกเปลี่ยน s-d ระหว่างการสะสมสปิน
และแมกนีไทเซชัน ต้องทำการพิจารณาค่าคงที่การแพร่ (D 0) ที่อยู่ในรูปฟังก์ชันอุณหภูมิเนื่องจากเป็น
p
ตัวแปรสำคัญที่ส่งผลต่อขนาดของสปินทอร์คซึ่งจะมีการลดลงตามระยะ λ J = 2¯hD 0 /J ที่มีความ
สัมพันธ์กับค่าคงที่การแพร่