Page 76 - Spin Transport and Spintronics

2.7 คำถามท้ายบท 77

2.7 คำถามท้ายบท

2.7.1 จงอธิบายการเกิดปรากฏการณ์สปินทอร์ค องค์ประกอบของสปินทอร์ค และจุดกำเนิดของการ
เกิด AST และ NAST

2.7.2 แบบจำลอง ZLF ที่อาศัยสมการลอยเลื่อนและการแพร่ มีข้อจำกัดอย่างไร ในการอธิบายพฤติ-
กรรมการส่งผ่านสปินในโครงสร้างวัสดุแม่เหล็ก และแบบจำลองทั่วไปของการสะสมสปินมีข้อดี ข้อเสีย

และความแตกต่างอย่างไรกับแบบจำลอง ZLF

2.7.3 พิจารณาผลของความหนาแน่นของกระแสไฟฟ้าที่ป้อนเข้าสู่โครงสร้างวัสดุแม่เหล็กที่มีต่อขนาด
ของสลอนเซวสกีทอร์ค โดยกำหนดให้กระแสไฟฟ้ามีความหนาแน่นระหว่าง 1 − 5 MA/cm 2

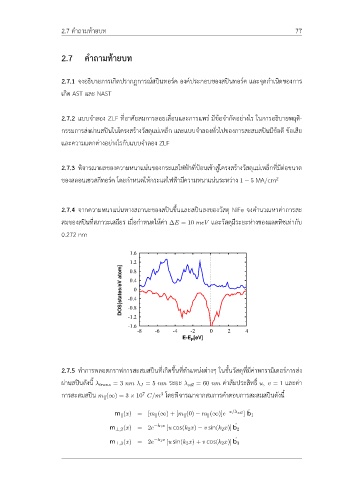
2.7.4 จากความหนาแน่นทางสถานะของสปินขึ้นและสปินลงของวัสดุ NiFe จงคำนวณหาค่าการสะ

สมของสปินที่สภาวะเสถียร เมื่อกำหนดให้ค่า ∆E = 10 meV และวัสดุมีระยะห่างของแลตทิซเท่ากับ
0.272 nm

1.6
1.2
DOS[states/eV atom] -0.4
0.8
0.4
0

-0.8
-1.2
-1.6
-8 -6 -4 -2 0 2 4
E-E [eV]
F

2.7.5 ทำการพลอตกราฟการสะสมสปินที่เกิดขึ้นที่ตำแหน่งต่างๆ ในชั้นวัสดุที่มีค่าพารามิเตอร์การส่ง

ผ่านสปินดังนี้ λ trans = 3 nm λ J = 5 nm ระยะ λ sdl = 60 nm ค่าสัมประสิทธิ์ u, v = 1 และค่า
การสะสมสปิน m (∞) = 3 × 10 C/m โดยพิจารณาจากสมการคำตอบการสะสมสปินดังนี้
7
3
∥
m (x) = [m (∞) + [m (0) − m (∞)]e −x/λ sdl ˆ
] b 1
∥
∥
∥
∥
ˆ
m ⊥,2 (x) = 2e −k 1 x [ucos(k 2 x) − vsin(k 2 x)]b 2
ˆ
m ⊥,3 (x) = 2e −k 1 x [usin(k 2 x) + vcos(k 2 x)]b 3