Page 66 - Spin Transport and Spintronics

2.5 แบบจำลองทั่วไปของการสะสมสปิน 67

p
เมื่อกำหนดให้ λ sdl = (1 − ββ )λ sf และคำตอบขององค์ประกอบขนานของการสะสมของสปินที่มี
′
ทิศทางไปตามทิศทางของ b 1 สามารถหาได้จากการแก้อนุพันธ์อันดับสองในสมการข้างต้น ดังนี้
ˆ

−x/λ sdl ˆ (2.19)
m (x) = [m (∞) + [m (0) − m (∞)]e ] b 1
∥ ∥ ∥ ∥
• ค่าการสะสมของสปินที่สภาวะสมดุล (m ∞)

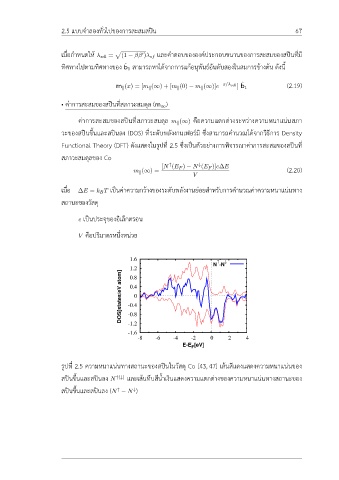
ค่าการสะสมของสปินที่สภาวะสมดุล m (∞) คือความแตกต่างระหว่างความหนาแน่นสภา
∥
วะของสปินขึ้นและสปินลง (DOS) ที่ระดับพลังงานเฟอร์มิ ซึ่งสามารถคำนวณได้จากวิธีการ Density

Functional Theory (DFT) ดังแสดงในรูปที่ 2.5 ซึ่งเป็นตัวอย่างการพิจารณาค่าการสะสมของสปินที่
สภาวะสมดุลของ Co

↓
[N (E F ) − N (E F )]e∆E
↑
m (∞) = (2.20)
∥
V
เมื่อ ∆E = k B T เป็นค่าความกว้างของระดับพลังงานย่อยสำหรับการคำนวณค่าความหนาแน่นทาง
สถานะของวัสดุ

e เป็นประจุของอิเล็กตรอน

V คือปริมาตรหนึ่งหน่วย

1.6 ↑ ↓
N -N
1.2
DOS[states/eV atom] -0.4
0.8
0.4
0

-0.8
-1.2
-1.6
-8 -6 -4 -2 0 2 4
E-E [eV]
F

รูปที่ 2.5 ความหนาแน่นทางสถานะของสปินในวัสดุ Co [43, 47] เส้นสีแดงแสดงความหนาแน่นของ

สปินขึ้นและสปินลง N ↑(↓) และเส้นทึบสีน้ำเงินแสดงความแตกต่างของความหนาแน่นทางสถานะของ
สปินขึ้นและสปินลง (N − N )
↓
↑